Isomorphism – graph comparisons

by Uwe B. Meding

Matching two graphs to see if they are identical is very complex. Mathematicians call the matching process graph isomorphism. In fact, it is not known to have a general solution at all. It has been determined that the complexity of a generic solution would put it almost into the class of NP (non-deterministic polynomial) problems. (See 1 and 2.) Problems that live in this class typically will take a decidedly long time to iterate through all required permutations to find a solution. For example, even a small graph with 100 vertices will exceed the enumeration required for all particles in the known universe. However, there are many graphs that define many more vertices, for example social networks or electronic circuits. Checking whether a given vertex bijection is an isomorphism would require an examination of all vertex pairs, which itself is not overwhelming. However, since one would need to check n! vertex bijections for determining general graph isomorphism, it makes this a difficult problem to solve.

There are a number of solutions to this problem – all of them involve adding additional pieces of information (anchor points if you will) to each graph such that it creates a situation were we move the problem away from the NP complexities of the generic problem. At that point, the problem becomes quite solvable.

Actually, in practice, this makes a lot of sense. A “pure” graph, with just vertices and edges without additional information is not very useful. However, by adding meaning to the graph, we are also defining anchor points which we can use to help the matching process.

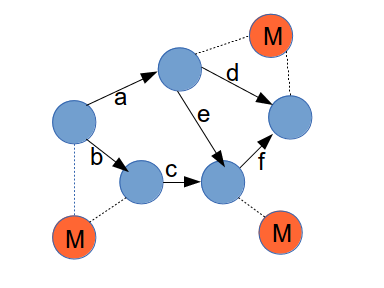
Roughly, the matching algorithm looks as follows:

We are sorting the vertices such that we are looking at the ones with the most edges first. Then we are attempting to match the vertices with the largest edge count. Any match will add more reference points into the graph. Then we start the process over again until we have all vertices and edges matched up. This process typically only takes a few iterations to complete.

A “master” vertex reference helps to identify nodes (vertices) that have the same meaning. For example, for a social network the master vertex may refer to a group and the vertices to individual people, with the edges referring to some interaction.